Media, moda, mediana, rango
La estadística más usada es el promedio, yhay tres formas de medirlo: la media, la mediana y la moda.
¿Por qué tres? Buena pregunta. Cada una te dará una forma diferente de ver los datos; dependiendo de la pregunta que quieras responder (o el argumento que quieras defender), cualquiera de las tres podría probar algo.
La media es la medida más usada para encontrar el promedio. De hecho, la gente siempre utiliza la palabra "promedio" para referirse a la "media." Encontrarla es simple: solo suma todos los números en los datos y divídelos por la cantidad de números.

La mediana es el número del medio en un grupo de datos. Sin embargo, los datos deben estar ordenados numéricamente (de mayor a menor o de menor a mayor) antes de encontrar este promedio. Si el número del medio está entre dos números, entonces encuentra la media entre esos dos (súmalos y divídelos entre 2).
Mediana: el número del medio en un grupo de datos.
La moda es probablemente la forma menos común de encontrar el promedio, y en la mayoría de los casos es la menos útil. Para encontrar la moda, solo encuentra el número que más se repite. Puede haber más de una moda, o ninguna.
Moda = número que más se repite.
Finalmente tenemos el rango. El rango NO es una medida de promedio; sin embargo, a menudo se utiliza como el promedio, porque es otra manera de medir un grupo de datos. El rango mide la "extensión" de los datos, qué tan alejados se encuentran el menor del mayor. Para encontrar el rango, resta el valor más pequeño del más grande.
Rango = valor más pequeño – valor más grande
Pero todo esto tendrá mucho más sentido si vemos algunos ejemplos. En nuestra encuesta de redes sociales, encontramos la mediana, la media y el rango de tiempo que cada grupo pasa en las páginas sociales por día.
| Tiempo dedicado a las redes sociales (horas/día) | Chicas | Chicos |
| Media | 2.20 | 1.01 |
| Mediana | 2.17 | 0.98 |
| Rango | 3.75 | 1.88 |
Como lo habíamos dicho, en promedio las chicas pasan al menos una hora más al día en estas páginas que los chicos. Tanto la media como la mediana para las chicas fue significativamente mayor a las de los chicos.
La puntuación de esta semana de "Mejores estudiantes de la Santiago"
Aquí tenemos la puntuación que los participantes de la materia Estadistica obtuvieron esta semana:
| Hernandez | 52 |
| Perez | 50 |
| Escalona | 47 |
| Rojas | 44 |
| Salazar | 39 |
| Barico | 38 |
| Alvarado | 36 |
| Salas | 32 |
Ahora encontremos los tres promedios y el rango para las puntuaciones de los concursantes.
| Estadística | Cómo encontrarla | Explicación |
| Media |  | Suma las puntuaciones y divídelas entre 8, el número total de concursantes. La media es 42.25. |
| Mediana |   | Primero ordena las puntuaciones, y después encuentra el valor del medio. En este grupo, el valor medio está entre 44 y 39, así que sumamos estos dos y los dividimos entre 2. |
| Moda | No tiene moda. | No hay ninguna puntuación que ocurra varias veces, así que no hay moda para este grupo de datos. |
| Rango | 52 – 32 = 20 | Resta el más pequeño del más grande. El rango es 20 puntos. |
Para este grupo de datos, solo hay dos medidas de promedio (no hay moda). Tanto la media como la mediana podrían usarse para describir el promedio. Si fueras Evan, ¿preferirías usar la media o la mediana? ¿Y si fueras Kate?
Cuidado: el rango de un grupo de datos NO mide el promedio de los datos.
DIAGRAMA DE TALLO Y HOJAS
Diagrama de tallo y hojas
Los diagramas de tallo y hojas se utilizan para analizar y exponer datos al mismo tiempo. Es una forma de relacionar los datos con otras variables.
Si volteas un diagrama de tallo y hoja, te queda algo como un histograma
Para hacer un diagrama de tallo y hojas, debes crear el "tallo" escribiendo los dígitos que representen los valores posicionales más grandes a la izquierda de una línea vertical. A la derecha, escribe los dígitos que sobren para crear las "hojas." Sí, suena abstracto.
Ejemplo.
Estas son las notas acumuladas de Estadistica :
90, 94, 53, 68, 79, 84, 87, 72, 70, 69, 65, 89, 85, 83, 72
El valor posicional más grande de todos los datos son las decenas. Estos dígitos serán nuestros tallos. Los escribimos de mayor a menor o de menor a mayor (de ambas formas funciona).

Ahora colocamos los demás dígitos de cada dato en la columna "Hojas." Por ejemplo, para trazar el valor 84, colocamos el 4 a la derecha del número 8. Allí también colocaremos todos los dígitos faltantes de los que obtuvieron una puntuación en los ochenta (si obtuviste 87, el 7 irá al lado del 4, si obtuviste 89, el 9 irá al lado del 7, y así sucesivamente).

Ahora arreglamos los números para que cada fila quede en orden numérico (de menor a mayor).

El diagrama de tallo y hoja es una forma conveniente de ver los datos en bruto. Usando este diagrama podemos ver que la mayoría de los estudiantes obtuvieron entre 70 y 80 puntos, y solo un estudiante sacó menos de 65.
Diagramas de caja
Los diagramas de caja son una forma útil de graficar datos divididos en cuatro cuartiles, cada uno con igual cantidad de valores. El diagrama de caja no grafica frecuencia ni muestra las estadísticas individuales, pero en ellos podemos ver claramente dónde se encuentra la mitad de los datos. Es un buen diagrama para analizar la asimetría en los datos.
A continuación, te dejamos algunas palabras que debes tener en cuenta cuando graficas diagramas de caja:
- Q1 – Cuartil 1, la mediana de la mitad menor de los datos.
- Q2 – Cuartil 2, la mediana de todos los datos.
- Q3 – Cuartil 3, la mediana de la mitad mayor de los datos.
- IQR – Rango intercuartil, la diferencia entre Q3 y Q1.
- Valores extremos – Los valores más pequeños y los más grandes de los datos.
Comencemos haciendo un diagrama de caja de la puntuación en la evaluacion del corte 1 y 2 de la materia Estadistica I:
90, 94, 53, 68, 79, 84, 87, 72, 70, 69, 65, 89, 85, 83, 72
Paso 1: ordena los datos de menor a mayor.
53 65 68 69 70 72 79 83 84 85 87 89 90 94
Paso 2: encuentra la mediana de los datos.
Llamado también cuartil 2 (Q2).
Paso 3: encuentra la mediana de los datos menores que Q2.
Este sería el cuartil menor (Q1).
Paso 4: encuentra la mediana de la data mayor que Q2.
Este sería el cuartil mayor (Q3).

Paso 5: encuentra los valores extremos.
Estos serían los valores más grandes y más pequeños.
Valores extremos = 53 y 94.
Paso 6: crea una recta real que contenga todos los datos.
Deja que se extienda un poco más allá de los valores extremos.

Paso 7: dibuja una caja de Q1 a Q3 divididas por una recta en Q2. Luego extiende los "bigotes" por cada lado de la caja hacia los valores extremos.
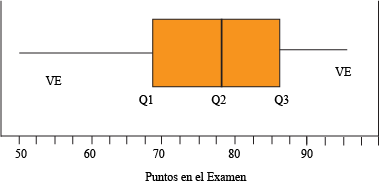
Esta gráfica está dividida en cuatro grupos distintos: el bigote menor, la mitad menor de la caja, la mitad mayor de la caja y el bigote mayor (el bigote mayor no se refiere a Jorge Negrete). Como en cada grupo hay una misma cantidad de datos, cada sección representa el 25% de los mismos.

A través de este diagrama vemos que el 50% de los estudiantes obtuvo entre 69 y 87 puntos, el 75% de los estudiantes obtuvo menos de 87 puntos y el 50% obtuvo más de 79. Si tu puntuación estuvo en el bigote mayor, siéntete orgulloso de ti mismo, ya que sacaste mejor nota que el 75% de tus compañeros. Si por el contrario, tu nota estuvo en el bigote menor, quizás tengas que estudiar un poco más.
Valores atípicos
Los valores atípicos son aquellos mucho más grandes o mucho más pequeños que el resto de los datos. Se representan con un punto en cualquier extremo del diagrama. En nuestro ejemplo no hubo ningún valor atípico; y aunque 53 parece ser mucho más pequeño que el resto, en realidad no fue lo suficientemente pequeño.
Para ser considerado un valor atípico, el valor debe ser:
- mayor que Q3 por, al menos, 1.5 veces el rango intercuartil (IQR), ó
- menor que Q1 por, al menos, 1.5 veces el IQR.
Los valores atípicos son aquellos que:
1.5(IQR) > Q3
1.5(IQR) < Q1
1.5(IQR) < Q1
A continuación, te presentamos los resultados individuales finales de salto de esquí masculino de los Juegos Olímpicos de invierno.
| 283.6 | 269.4 | 262.2 | 261.1 | 246.7 |
| 245.5 | 239.2 | 233.7 | 230.3 | 227.9 |
| 226.4 | 225.5 | 224.1 | 223.6 | 222.3 |
| 221.4 | 217.8 | 217.2 | 216.9 | 211.6 |
| 211.4 | 208.5 | 204.9 | 202.7 | 202.4 |
| 200.5 | 198.5 | 182.4 | 111 |
Los cuartiles quedan así: Q1 sería 208.5, Q2 sería 222.3 y Q3 sería 236.45. La puntuación más baja (111) parece ser un valor atípico, ya que es mucho más pequeña que el resto de los datos. Sin embargo, no podemos estar seguros hasta que saquemos las cuentas.
Primero debemos calcular el IQR, que es Q3 – Q1. Luego lo multiplicamos por 1.5 para obtener el número que necesitamos para saber si hay algún valor atípico.
IQR = 236.45 – 208.50 = 27.95
1.5(IQR) = 1.5(27.95) = 41.93
208.5 – 41.93 = 166.57
Para que el número en cuestión (111) califique como un valor atípico, debe ser menor a 166.57, que es la diferencia entre Q1 (208.5) y 41.93.
¡Sí, es! Como 111 es menor a 166.57, entonces declaramos oficialmente a 111 como un valor atípico. Al hacer el diagrama de caja, representamos a 111 con un punto y extendemos el bigote menor solo hasta el siguiente valor menor (que sería 182.4).

Quizá deberíamos verificar que no haya ningún valor atípico hacia la mitad mayor de los datos.
236.45 + 41.93 = 278.38
Hay un valor cerca de 278.38, así que éste también es un valor atípico.



