MEDIDAS
DE ASIMETRÍA
Y
KURTOSIS
Las medidas de distribución nos permiten identificar la forma en que se separan o aglomeran los valores de acuerdo a su representación gráfica. Estas medidas describen la manera como los datos tienden a reunirse de acuerdo con la frecuencia con que se hallen dentro de la información. Su utilidad radica en la posibilidad de identificar las características de la distribución sin necesidad degenerar el gráfico. Sus principales medidas son la Asimetría y la Kurtosis.
1. ASIMETRÍA
Esta medida nos permite identificar si los datos se distribuyen de forma uniforme alrededor del punto central (Media aritmética). La asimetría presenta tres estados diferentes, cada uno de los cuales define de forma concisa como están distribuidos los datos respecto al eje de asimetría. Se dice que la asimetría es positiva cuando la mayoría de los datos se encuentran por encima del valor de la media aritmética, la curva es Simétrica cuando se distribuyen aproximadamente la misma cantidad de valores en ambos lados de la media y se conoce como asimetría negativa cuando la mayor cantidad de datos se aglomeran en los valores menores que la media.
Ejemplo
El Coeficiente de asimetría, se representa mediante la ecuación matemática,
Donde (g1) representa el coeficiente de asimetría de Fisher, (Xi) cada uno de los valores, (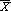
) la media de la muestra y (ni) la frecuencia de cada valor.
) la media de la muestra y (ni) la frecuencia de cada valor.
Los resultados de esta ecuación se interpretan:
(g1 = 0): Se acepta que la distribución es Simétrica, es decir, existe aproximadamente la misma cantidad de valores a los dos lados de la media. Este valor es difícil de conseguir por lo que se tiende a tomar los valores que son cercanos ya sean positivos o negativos (± 0.5).
(g1 > 0): La curva es asimétricamente positiva por lo que los valores se tienden a reunir más en la parte izquierda que en la derecha de la media.
(g1 < 0): La curva es asimétricamente negativa por lo que los valores se tienden a reunir más en la parte derecha de la media.
Desde luego entre mayor sea el número (Positivo o Negativo), mayor será la distancia que separa la aglomeración de los valores con respecto a la media.
Coeficiente de asimetría de Fisher
El coeficiente de asimetría de Fisher CAF evalúa la proximidad de los datos a su media x.
Cuanto mayor sea la suma ∑(xi–x)3, mayor será la asimetría.
Sea el conjunto X=(x1, x2,…, xN), entonces la fórmula de la asimetría de Fisher es:
- Si CAF<0: la distribución tiene una asimetría negativa y se alarga a valores menores que la media.
- Si CAF=0: la distribución es simétrica.
- Si CAF>0: la distribución tiene una asimetría positiva y se alarga a valores mayores que la media.
Coeficiente de asimetría de Bowley
El coeficiente de asimetría de Bowley CAB toma como referencia los cuartiles para determinar si la distribución es simétrica o no. Para aplicar este coeficiente, se supone que el comportamiento de la distribución en los extremos es similar. Sea el conjunto X=(x1, x2,…, xN), la asimetría de Bowley es:
Esta fórmula viene de:
Recordemos que la mediana (Me) es lo mismo que el segundo cuartil (Q2).
Por lo que la fórmula del coeficiente de asimetría de Bowley también se puede escribir así:
- Si CAB<0: la distribución tiene una asimetría negativa, puesto que la distancia de la mediana al primer cuartil es menor que al tercero.
- Si CAB=0: la distribución es simétrica, ya que el primer y tercer cuartil están a la misma distancia de la mediana.
- Si CAB>0: la distribución tiene una asimetría positiva, ya que la distancia de la mediana al tercer cuartil es mayor que al primero.
2. KURTOSIS
Esta medida determina el grado de concentración que presentan los valores en la región central de la distribución. Por medio del Coeficiente de Kurtosis, podemos identificar si existe una gran concentración de valores (Leptocúrtica), una concentración normal (Mesocúrtica) ó una baja concentración (Platicúrtica).
Ejemplo:
Para calcular el coeficiente de Kurtosis se utiliza la ecuación:
Donde (g2) representa el coeficiente de Kurtosis, (Xi) cada uno de los valores, (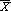) la media de la muestra y (ni) la frecuencia de cada valor. Los resultados de esta fórmula se interpretan:
) la media de la muestra y (ni) la frecuencia de cada valor. Los resultados de esta fórmula se interpretan:
(g2 = 0) la distribución es Mesocúrtica: Al igual que en la asimetría es bastante difícil encontrar un coeficiente de Curtosis de cero (0), por lo que se suelen aceptar los valores cercanos (± 0.5 aprox.).
(g2 > 0) la distribución es Leptocúrtica
(g2 < 0) la distribución es Platicúrtica
Cuando la distribución de los datos cuenta con un coeficiente de asimetría (g1 = ±0.5) y un coeficiente de Curtosis de (g2 = ±0.5), se le denomina Curva Normal. Este criterio es de suma importancia ya que para la mayoría de los procedimientos de la estadística de inferencia se requiere que los datos se distribuyan normalmente.
La principal ventaja de la distribución normal radica en el supuesto que el 95% de los valores se encuentra dentro de una distancia de dos desviaciones estándar de la media aritmética (Fig.5-3); es decir, si tomamos la media y le sumamos dos veces la desviación y después le restamos a la media dos desviaciones, el 95% de los casos se encontraría dentro del rango que compongan estos valores.
La teoria han sido extraídas de los libros Estadística para administradores escrito por Alan Wester de la editorial McGraw-Hill y el libro Estadística y Muestreo escrito por Ciro Martínez editorial Ecoe
